What is the Difference Between Type1 and Type2 With Regards to Reactive Power, Apparent Power, and Other Formulas?
Selecting formulas for calculating apparent power and reactive power
There are several types of power—active power, reactive power, and apparent power.
Generally, the following equations are satisfied:
Active power P = UIcosθ (1)
Reactive power Q = UIsinθ (2)
Apparent power S = UI (3)
In addition, these power values are related to each other as follows:
(Apparent power S)2 = (Active power P)2 + (Reactive power Q)2 (4)
U: Voltage RMS
I: Current RMS
θ: Phase between current and voltage
Three-phase power is the sum of the power values in the individual phases.
These defining equations are only valid for sinewaves. In recent years, there has been an increase in measurements of distorted waveforms, and users are measuring sinewave signals less frequently. Distorted waveform measurements provide different measurement values for apparent power and reactive power depending on which of the above defining equations is selected. In addition, because there is no defining equation for power in a distorted wave, it is not necessarily clear which equation is correct. Therefore, three different formulas for calculating apparent power and reactive power are provided with the WT3000.
TYPE 1 (method used in normal mode with older WT Series models)
With this method, the apparent power for each phase is calculated from equation (3), and reactive power for each phase is calculated from equation (2). Next, the results are added to calculate the power.
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection: SΣ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power for three-phase four-wire connection: QΣ=Q1+Q2+Q3
TYPE 2
The apparent power for each phase is calculated from equation (3), and the results are added together to calculate the three-phase apparent power (same as in TYPE1). Three-phase reactive power is calculated from three-phase apparent power and three-phase active power using equation (4).
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection: SΣ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power for three-phase four-wire connection:
TYPE 3 (method used in harmonic measurement mode with WT1600 and PZ4000)
This is the only method in which the reactive power for each phase is directly calculated using equation (2). Three-phase apparent power is calculated from equation (4).
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection: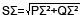
Reactive power for three-phase four-wire connection: QΣ=Q1+Q2+Q3
Also, the power factor is calculated as P/S. By selecting the formula TYPE for apparent power and reactive power, the value of the three-phase total power factor λΣ also changes.
Supplement:
<TYPE 1>
This is equivalent to the normal mode formula used by the conventional WT series instruments (WT1600, WT2000, etc.).
QΣ=Q1+Q2+Q3
*s1, s2, and s3 express the polarity of Q1, Q2, and Q3 of the reactive power of each phase. When current leads or lags the voltage, it is accompanied by a “-“ sign (reactive power is a negative value), or a “+” sign (reactive power is a positive value), respectively.
QΣ is calculated from the reactive power of each phase Q1, Q2, and Q3 with the signs.
With TYPE1 there can be cases where, if the waveform is distorted, polarity determination (lead/lag is detection) may not be successful, and as a result the QΣ value may not be calculated correctly. For polarity determination, specifications such as the following are listed in the catalog.
Lead/Lag Detection in WT3000 specifications:
The phase lead and lag are detected correctly when the voltage and current signals are both sine waves, the lead/lag is 50% of the range rating (or 100% for crest factor 6), the frequency is between 20 Hz and 10 kHz, and the phase angle is ±(5°to 175°) or more.
<TYPE 2> (New mode not dependent on leading phase/lagging phase detection error)
For Type 2 the method is changed and QΣ is calculated from SΣ and PΣ, so this problem does not occur.

For example,
In order to improve the power factor as a measure against harmonic current in the switching power supply, to confirm the effect of the power factor on the current distortion waveform → TYPE1 and TYPE2 are applied.
<TYPE 3>
A mode for direct measurement of reactive power through harmonic measurement (same as WT1600 and PZ4000).
Since this mode involves harmonic measurements, measurements can be taken for each harmonic component. Since the results reflect each frequency component, the reactive power Q for each order is correct. Also, the QΣ is a simple summation so the sum of each order QΣ is also correct. The active power and reactive power of the harmonic components are computed, so the mode allows for more accurate calculation of phase information by order.
There are several types of power—active power, reactive power, and apparent power.
Generally, the following equations are satisfied:
Active power P = UIcosθ (1)
Reactive power Q = UIsinθ (2)
Apparent power S = UI (3)
In addition, these power values are related to each other as follows:
(Apparent power S)2 = (Active power P)2 + (Reactive power Q)2 (4)
U: Voltage RMS
I: Current RMS
θ: Phase between current and voltage
Three-phase power is the sum of the power values in the individual phases.
These defining equations are only valid for sinewaves. In recent years, there has been an increase in measurements of distorted waveforms, and users are measuring sinewave signals less frequently. Distorted waveform measurements provide different measurement values for apparent power and reactive power depending on which of the above defining equations is selected. In addition, because there is no defining equation for power in a distorted wave, it is not necessarily clear which equation is correct. Therefore, three different formulas for calculating apparent power and reactive power are provided with the WT3000.
TYPE 1 (method used in normal mode with older WT Series models)
With this method, the apparent power for each phase is calculated from equation (3), and reactive power for each phase is calculated from equation (2). Next, the results are added to calculate the power.
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection: SΣ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power for three-phase four-wire connection: QΣ=Q1+Q2+Q3

TYPE 2
The apparent power for each phase is calculated from equation (3), and the results are added together to calculate the three-phase apparent power (same as in TYPE1). Three-phase reactive power is calculated from three-phase apparent power and three-phase active power using equation (4).
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection: SΣ=S1+S2+S3(=U1×I1+U2×I2+U3×I3)
Reactive power for three-phase four-wire connection:

TYPE 3 (method used in harmonic measurement mode with WT1600 and PZ4000)
This is the only method in which the reactive power for each phase is directly calculated using equation (2). Three-phase apparent power is calculated from equation (4).
Active power for three-phase four-wire connection: PΣ=P1+P2+P3
Apparent power for three-phase four-wire connection:
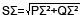
Reactive power for three-phase four-wire connection: QΣ=Q1+Q2+Q3
Also, the power factor is calculated as P/S. By selecting the formula TYPE for apparent power and reactive power, the value of the three-phase total power factor λΣ also changes.
Supplement:
<TYPE 1>
This is equivalent to the normal mode formula used by the conventional WT series instruments (WT1600, WT2000, etc.).
QΣ=Q1+Q2+Q3

*s1, s2, and s3 express the polarity of Q1, Q2, and Q3 of the reactive power of each phase. When current leads or lags the voltage, it is accompanied by a “-“ sign (reactive power is a negative value), or a “+” sign (reactive power is a positive value), respectively.
QΣ is calculated from the reactive power of each phase Q1, Q2, and Q3 with the signs.
With TYPE1 there can be cases where, if the waveform is distorted, polarity determination (lead/lag is detection) may not be successful, and as a result the QΣ value may not be calculated correctly. For polarity determination, specifications such as the following are listed in the catalog.
Lead/Lag Detection in WT3000 specifications:
The phase lead and lag are detected correctly when the voltage and current signals are both sine waves, the lead/lag is 50% of the range rating (or 100% for crest factor 6), the frequency is between 20 Hz and 10 kHz, and the phase angle is ±(5°to 175°) or more.
<TYPE 2> (New mode not dependent on leading phase/lagging phase detection error)
For Type 2 the method is changed and QΣ is calculated from SΣ and PΣ, so this problem does not occur.

For example,
In order to improve the power factor as a measure against harmonic current in the switching power supply, to confirm the effect of the power factor on the current distortion waveform → TYPE1 and TYPE2 are applied.
<TYPE 3>
A mode for direct measurement of reactive power through harmonic measurement (same as WT1600 and PZ4000).
Since this mode involves harmonic measurements, measurements can be taken for each harmonic component. Since the results reflect each frequency component, the reactive power Q for each order is correct. Also, the QΣ is a simple summation so the sum of each order QΣ is also correct. The active power and reactive power of the harmonic components are computed, so the mode allows for more accurate calculation of phase information by order.
Related Products & Solutions
Power Analyzers and Power Meters
Yokogawa, the world's largest manufacturer of energy and power analyzers and meters, provides a broad choice of digital power analyzers to satisfy all requirements.
Precision Power Analyzer WT3000
With 0.02% accuracy and 1MHz bandwidth, the WT3000 delivers where the highest precision measurements are required. It is the industry standard for R&D work on inverters, motor drives, lighting systems and electronic ballasts, UPS systems, aircraft power, transformer testing, and other power conversion devices.
Top

